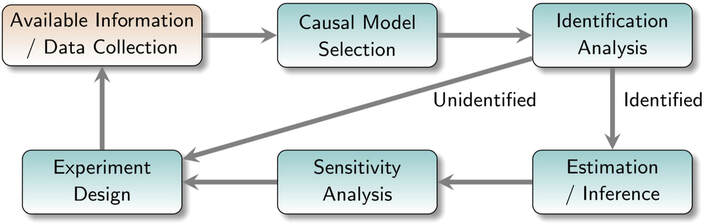
Causal Learning Paradigm
Majority of questions in science are of a causal nature and for the most part, cannot be answered solely based on associations in observational data. This includes questions about the health effects of a certain treatment in the field of medicine, the impact of a certain human activity on climate change in natural sciences, or the consequences of a new policy on economic indices. A common approach used for answering questions of this type is to describe the quantity of interest as a parameter of the distribution of the available data, and then use a learning scheme to estimate that parameter. However, in many cases, the estimated parameter is not the causal parameter of interest. In fact, the causal parameter of interest may not be even identifiable from the available data. This results in a systematic bias in the estimated parameter (i.e., a bias that does not vanish as sample size increases) and leads to misleading conclusions. The literature of modern causal inference advocates the use of a causal learning paradigm. The main idea of this paradigm is to consider a causal model for the system that encompasses both factual and counterfactual realizations of the system, and then investigate what aspects of this model is captured by the observational data. In what follows, I present my view of the main components of this paradigm. A diagram of this paradigm is shown in the figure above. In this framework, given the available information about the setup under study and data collected from the system, the following path is followed.
- Causal Model Selection: The first step is to choose a causal model for the system. A common way to represent the causal model is via graphs, although in general, the model does not need to be graphical. A graphical causal model can be chosen based on the available information, such as expert knowledge, or it can be learned from data, a process referred to as causal discovery, or causal structure learning. A causal graph represents the causal relationships among the variables in a system (e.g., how different regions of the brain are causally related to each other). Besides aiding in causal inference, a graphical causal model can be instrumental in addressing recently emerging challenges in learning systems such as fairness and interpretability.
- Identification Analysis: The goal of this step is to decide whether the causal parameter of interest is identifiable from the available data under the posited causal model. In other words, identification analysis tells us assuming the causal model is true, whether the answer to our question can be found in our data. As mentioned earlier, unfortunately this step is often missing in the existing learning pipelines. A particularly challenging case is when only observational data is available. In this case, identification analysis is concerned with finding whether the causal parameter, which is a functional of the full data distribution, can also be captured as a functional of the observed data distribution. For instance, consider the causal question of evaluating the effect of class size on students' test scores. Here, the quantity of interest is how the test scores change if all students were assigned to large classes compared to the case that all students were assigned to small classes. Therefore, this quantity is a parameter of a distribution that contains both potential outcomes of students' test scores. However, the available observational data contains only one outcome for each student coming from a mix of students from small and large classes. Moreover, unobserved factors, such as socioeconomic factors, could influence both whether a student is in a large or a small class, as well as their performance.
- Estimation/Inference: When the identification analysis determines that the causal parameter of interest is identifiable, the next step is to design an estimator for the parameter. Here, the goal is to find an estimator which is as robust and efficient as possible. Estimation, and specifically, nonparametric estimation has been one of the main foci of the machine learning literature. However, up until recently, the machine learning tools have been mostly ignored in the literature of causality.
- Sensitivity Analysis: A crucial step in a reliable causal learning paradigm is sensitivity analysis. Here, the goal is to evaluate how sensitive the resulting conclusions of the inference step are to the variations in the chosen model in Step 1. If the sensitivity is high, new data must be collected based on performing experiments to examine different aspects of the selected model.
- Experiment Design: The need for designing experiments can also arise when the identification analysis determines that the parameter is not identifiable from the data at hand. In this case, new data must be collected with the goal of enriching our information about aspects of the model needed for identification. This is usually done by intervening in the system and examining the system under intervention. Experiment design refers to the task of choosing the type and targets for interventions which lead to maximum information under the model's constraints.